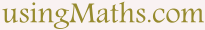Vectors and Matrices in Python
Vectors and matrices are core concepts in linear algebra and play a central role in many Python applications, particularly in graphics, animation, simulations, and game development. Understanding how to represent and manipulate vectors and matrices in Python provides a strong mathematical foundation for working with coordinate systems, transformations, and motion in two and three dimensions.
This page introduces vectors and matrices in Python and demonstrates how common vector and matrix operations can be implemented directly in code. The emphasis is on clarity and mathematical correctness rather than reliance on external libraries, making the techniques suitable for learning and educational use.
Understanding Vectors and Matrix Operations in Python
In programming, a matrix is often represented as an "array within an array." Mastery of Python matrix operations allows you to perform rotations, scaling, and translations in 2D and 3D space programmatically.
Defining Your Data Structures
To begin, we represent our mathematical objects as standard Python arrays. A vector is treated as a specific type of matrix—one with a single column.
- Scalar: A single numerical value.
- Vector: A list of numbers representing magnitude and direction.
- Matrix: A rectangular grid of numbers arranged in rows and columns.
Representing Vectors in Python
In Python, vectors are commonly represented using arrays or simple objects. A vector may describe a position, displacement, velocity, or direction, depending on the context in which it is used.
For example, a two-dimensional vector can be stored as an array containing its components along the x- and y-axes. This representation allows standard vector operations in Python, such as addition, subtraction, and scaling, to be implemented using straightforward functions.
Working with vectors in this way helps reinforce the connection between linear algebra concepts and practical Python programming.
Vector Operations in Python
Basic vector operations form the foundation for more advanced mathematical techniques used in graphics and animation.
Common vector operations include:
- Vector addition and subtraction
- Scalar multiplication
- Calculating magnitude (length)
- Normalising a vector
Implementing these vector operations in Python allows programmers to model motion, forces, and directional changes accurately. These techniques are especially useful in canvas-based graphics and interactive applications where precise control over movement is required.
Representing Matrices in Python
Matrices extend vector ideas and are essential for handling transformations such as rotation, scaling, and translation. In Python, matrices are typically represented as two-dimensional arrays, where each inner array corresponds to a row of the matrix.
This approach closely mirrors the mathematical definition of a matrix and makes it easier to translate linear algebra formulas directly into Python code. It also prepares students for more advanced topics such as matrix multiplication and coordinate transformations.
Matrix Operations in Python
Matrix operations in Python allow complex transformations to be expressed concisely and applied consistently.
Typical matrix operations include:
- Matrix addition and subtraction
- Matrix multiplication
- Multiplying a matrix by a vector
- Calculating determinants and inverses (for square matrices)
Since matrices can be represented as arrays of arrays. With Python, you can easily perform:
- Matrix Addition and Subtraction - Combine or reduce values element by element.
- Matrix Multiplication - Essential for scaling, rotating, and skewing objects in graphics.
- Determinant and Inverse Matrix - Useful for solving systems of equations and advanced transformations.
Example: Python Algorithm for Multiplication of Matrices >>>
These matrix operations are central to linear algebra and are widely used in computer graphics, physics simulations, and game engines. Implementing them manually in Python strengthens understanding of both the mathematics and the underlying algorithms.
Vectors as Matrices
Vectors can be treated as single-row or single-column matrices. This makes it easy to apply linear algebra techniques in Python:
- Representing points in 2D and 3D space.
- Performing dot products and cross products.
- Applying transformations for animations and simulations.
Image Manipulation with Matrices
Beyond math, matrices are widely used in Python image manipulation. By applying matrix operations, you can:
- Rotate images clockwise or counterclockwise.
- Scale pictures up or down.
- Skew and mirror graphics for creative effects.
- Combine with HTML Canvas or SVG graphics for dynamic rendering.
Using Vectors and Matrices for Graphics
Vectors and matrices are particularly important in web graphics, including HTML5 canvas and SVG. Vectors can represent positions and directions, while matrices are used to apply transformations such as rotation, scaling, and reflection.
For example, a transformation matrix can be used to rotate a shape about the origin or scale an object uniformly across the screen. Combining vector and matrix techniques allows complex graphical effects to be achieved using relatively simple Python code.
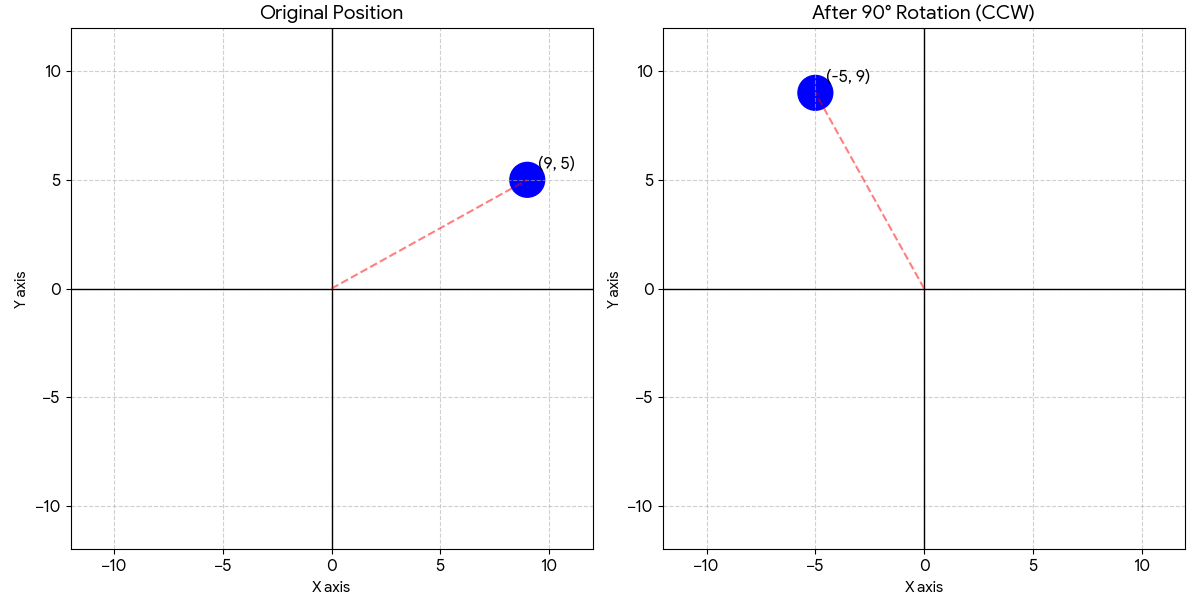
Example: Python Algorithm for rotation of vectors using a rotation matrix on a 2D plane >>>
Understanding these ideas also provides a solid introduction to the mathematics behind animation, game development, and computer graphics more generally.
Educational Focus and Further Study
The methods presented here are intended for educational use at a tertiary level. By coding vectors and matrices directly in Python, students gain a deeper appreciation of linear algebra concepts and how they are applied in real programming contexts.
An obvious improvement and practice exercise or fun activity is including checks in the Python algorithm to make sure the supplied matrices meet the dimensional requirement for matrix multiplication.
Once these fundamentals are understood, learners can more confidently move on to advanced topics such as transformation pipelines, three-dimensional graphics, and specialised Python libraries that build upon the same mathematical principles.
Practical Applications
- Web Development: Enhance animations and transitions with matrix transformations.
- Game Design: Use vectors and matrices for physics simulations and character movement.
- Educational Projects: Build interactive math tutorials and visualizations.
Summary: Vectors and Matrices in Python
Vectors and matrices are fundamental tools in mathematics and computer science. In Python, they provide a powerful way to perform matrix operations and vector calculations that support everything from graphics transformations to image manipulation. This tutorial explored how to implement matrix addition, subtraction, multiplication, determinants, and inverses directly in Python.
- Vectors and matrices are fundamental tools in Python programming for graphics and simulations
- Python arrays provide a clear and effective way to represent vectors and matrices
- Implementing vector and matrix operations reinforces linear algebra concepts
- These techniques form the mathematical basis of canvas graphics, animation, and game development
Mastering vectors and matrices in Python opens the door to advanced graphics transformations, image manipulation, and mathematical problem solving. Whether you’re a student learning linear algebra or a developer building interactive web applications, these concepts are essential for creating dynamic, visually engaging projects.
Python Code for Multiplication of Matrices - Module File
# define a class
class MatrixMultiplication:
def __init__(self):
self.i = 0
# Matrix multiplication in JavaScript
# Follows same steps as you would do on paper
#
# Warning: No checks have been done to ensure the
# dimension of both matrices are in order for multiplication
#
def multiplyMatrices(self, a, b):
result = []
for i in range(len(a)):
row_values = []
for j in range(len(b[0])):
m_sum = 0
for k in range(len(b)):
m_sum += a[i][k] * b[k][j]
row_values.append(m_sum)
result.append(row_values)
return result
Python Code for Multiplication of Matrices - Main Class
from MultiplyMatrix import MatrixMultiplication
import math
matrix_A = [
[5, 0, 2],
[1, 3, 8],
[6, 1, 4]
]
matrix_B = [
[2, 0, 0],
[0, 2, 0],
[0, 0, 2]
]
mul_mat = MatrixMultiplication()
result = mul_mat.multiplyMatrices(matrix_A, matrix_B)
# print style inherently assumes same dimension for matrices A, B and result
print_result = "[ "
print_result += " "
print_result += "[ "
print_result += " ["
rows_centre = math.ceil(len(result) / 2) - 1
for i in range(len(result)):
print_result += "\n [" + ", ".join(str(n) for n in matrix_A[i]) + "]"
if i == rows_centre:
print_result += " X "
else:
print_result += " "
print_result += " [" + ", ".join(str(n) for n in matrix_B[i]) + "]"
if i == rows_centre:
print_result += " = "
else:
print_result += " "
print_result += " [" + ", ".join(str(n) for n in result[i]) + "]"
print_result += "\n] "
print_result += " "
print_result += "] "
print_result += " ]"
print(print_result)
Python Code for Rotation of Matrices - Module File
from MultiplyMatrix import MatrixMultiplication
import math
# define a class
class MatrixRotation(MatrixMultiplication):
def __init__(self):
super().__init__()
# Matrix rotation in Python
def rotateAMatrix(self, matrix, angle):
angle_in_radians = angle * (math.pi / 180)
# 3D rotation matrix - the extra zeroes (0) and ones (1) are there for unity matrix balance
rotation_matrix = [
[math.cos(angle_in_radians), -math.sin(angle_in_radians), 0, 0],
[math.sin(angle_in_radians), math.cos(angle_in_radians), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]
return self.multiplyMatrices(rotation_matrix, matrix)
Python Code for Rotation of Matrices - Main Class
from RotateMatrix import MatrixRotation
import math
vector_A = [
[9], # x-coordinate
[5], # y-coordinate
[0], # z-coordinate - use zero(0) for 2D special systems
[1] # balance for 4x4 rotation matrix
]
angle = -90
rot_mat = MatrixRotation()
result = rot_mat.rotateAMatrix(vector_A, angle)
# do a formatted print style
spacing_span = " "
spacing_span += " "
spacing = spacing_span
print_result = spacing
print_result += "[ [\n"
rows_centre = math.ceil(len(result) / 2) - 1
for i in range(len(result)):
if i == rows_centre:
print_result += "A " + str(angle) + " rotation of "
spacing = " "
else:
spacing = spacing_span
print_result += spacing + " [" + ", ".join(str(n) for n in vector_A[i]) + "]"
if i == rows_centre:
print_result += " = "
else:
print_result += " "
print_result += " [" + ", ".join(str(n) for n in result[i]) + "]\n"
print_result += spacing
print_result += "] ]"
print(print_result)